
操作说明:
转动手轮,使齿轮转动一周,观察两个齿轮运动情况。
产品简介:
这是轮子悖论问题。轮子悖论出自古希腊著作《机械》,提出者为亚里士多德。有大小两个轮子,其中小轮子(r)附着于大轮子(R)中间。大轮子滚动一周,小轮子也正好滚动一周,这样说的话,它们的周长就是一样的。但这与两个轮子有着不同的直径,即不同的周长是相互矛盾的。
视频演示:
原 理:
有两个轮子,其中一个轮子在另一个轮子中间,它们有着不同的直径。它们底边上某点所走过的路径都是直线,乍一看,这两条直线似乎等于两轮的周长。但是这两条直线有着相同的长度,因此两个轮子的周长必定相同,这与两个轮子有着不同的直径是相互矛盾的,这就是所谓的轮子悖论。
这个悖论存在的漏洞就在于,假定小一点的轮子的进行轨迹为其周长。事实上,对两个轮子来说,想要做出完全相同的运动是不可能的。小一点的轮子并没有如图1所示从点3转动到点4,而是被大轮子拽着沿着这条直线前进。
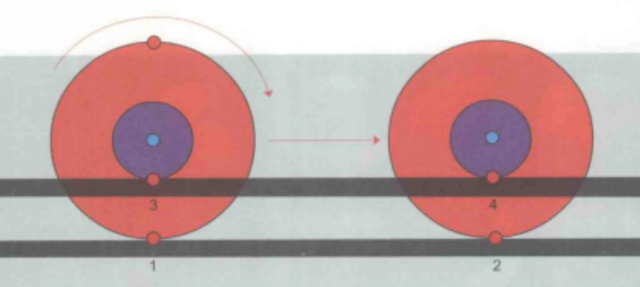
从物理学角度来看,如果两个半径不同的同心轮子沿着一条平行线转动,那么其中至少会有一个打滑。如果利用齿轮系统防止打滑,那么轮子就会出现被卡住的情况。
在当代类似的实验中,这种情况通常会在司机将车停在路边时无意中发生。实验发现,尽管轮毂不断转动并发出刺耳声音,但汽车外胎并没有出现打滑的情况。
从数学角度来看,内圆的点的数量与外圆的点的数量是完全一样的,即这两个圆之间存在着一种双射的情况(一种对应关系)。这并不能运用到轮子实体上,因为它们是由离散的原子组成的。因此在车轮的密度、宽度与厚度等都相同的情况下(不同的只是他们之间的半径),较大车轮的原子数量肯定要更多一些
应 用:
轮子悖论在多个领域中有着广泛的应用,主要包括数学、物理学和工程学等领域。
数学领域
轮子悖论在数学领域的应用主要体现在逻辑和几何学中。亚里士多德的轮子悖论是一个经典的逻辑悖论,它揭示了在某些情况下,直观上的直观感受与逻辑推理之间的矛盾。这个悖论帮助数学家们更好地理解逻辑推理的复杂性和局限性,促进了逻辑学和数学逻辑的发展。
物理学领域
在物理学中,轮子悖论的应用主要体现在对运动和力的理解上。伽利略通过将圆形纸片换成正多边形,并逐渐增加边数,最终无限接近于圆,解释了小圆在大圆滚动时的实际运动状态。这种解释方法不仅解决了悖论,还为后来的微积分和运动学研究提供了重要的启示。
工程学领域
在工程学中,轮子悖论的应用主要体现在机械设计和运动分析上。工程师们通过理解轮子悖论,可以更好地设计车轮和其他旋转部件,确保它们在实际应用中的稳定性和效率。此外,轮子悖论还促进了对齿轮传动和机械传动系统的深入研究,提高了机械设备的精度和可靠性。